Diffraction
Introduction
One thing that even the average professional astronomer might not fully appreciate is that Spitzer's images are diffraction-limited. Every telescope in space can produce images limited only by the effects of diffraction -- this effect is stronger for longer wavelengths and smaller telescopes -- but diffraction will only be noticed if the camera on the telescope samples the telescope's output finely enough. This is more often a problem for telescopes in the infrared rather than the optical, because the wavelengths of infrared light are longer.
Telescopes in space produce images that are not degraded by passage of incoming light through the Earth's atmosphere. Only the intrinsic properties of the telescope optics affect the quality of the image. A fundamental limit to the resolution is set by the properties of light itself, specifically the diffraction limit. This effect is stronger for longer wavelengths and smaller telescopes. Diffraction will only be noticed if the camera on the telescope samples the telescope's output finely enough.
Recall that, for the diffraction pattern through a circular aperture of diameter (d), the location of the first minimum (theta) is given by sin(theta) = 1.22 lambda/d where lambda is the wavelength of light under consideration, in the same units as d. For Hubble (d=2.4m), and optical light (500 nm) this works out to be theta=~2x10^(-7) rad=0.05 arcsec. Spitzer has long wavelengths and a small aperture in comparison to Hubble! Now, theta works out to be two orders of magnitude larger, ~3x10^(-5) rad=7.1 arcsec for 24 microns.
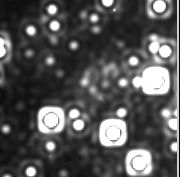Actual image from NICMOS on HST showing diffraction rings (Airy rings) around stars at the Galactic Center.
Diffraction and Spitzer
Most of Spitzer's images will show diffraction rings because of the telescope's small size (85 cm) and long observing wavelengths (8-160 microns). The size of a patch on the sky (pixel size) that Spitzer measures increases from 1.2 arcseconds at 3.6 microns to 15 arcseconds at 160 microns.
Theoretical (pre-launch) Spitzer image pattern (PSF or point spread function) shown using two different brightness scalings.
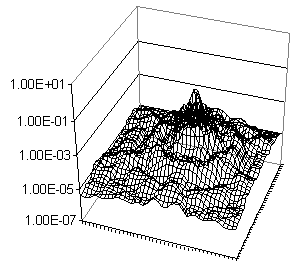Theoretical (pre-launch) Spitzer PSF in 3-D
