Finding the diameter of a region we care about

From CoolWiki
Jump to navigationJump to search

Multiple ways to measure the diameter.

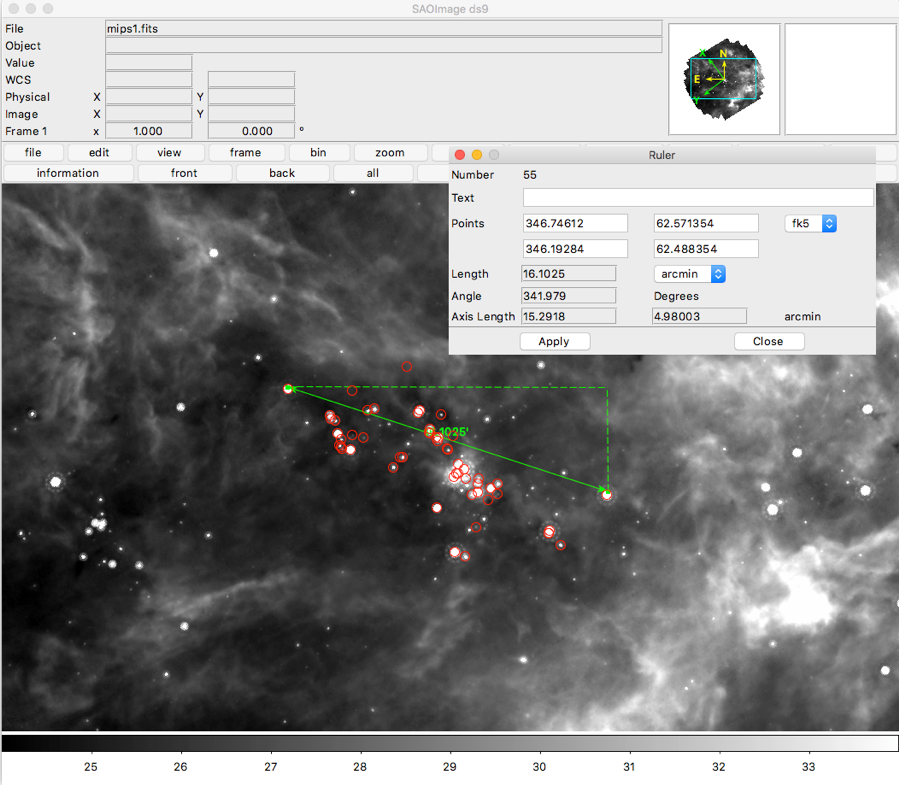
(1) load our image into ds9. Load our regions file of interesting objects onto it. Create a region that is a ruler. Click and drag between the extremes to measure the length. Double click on the region to bring up a pop-up that shows you the length of the region you have created. Change the units if you want. I get 16 arcmin for the size of our region.

Distance1.png

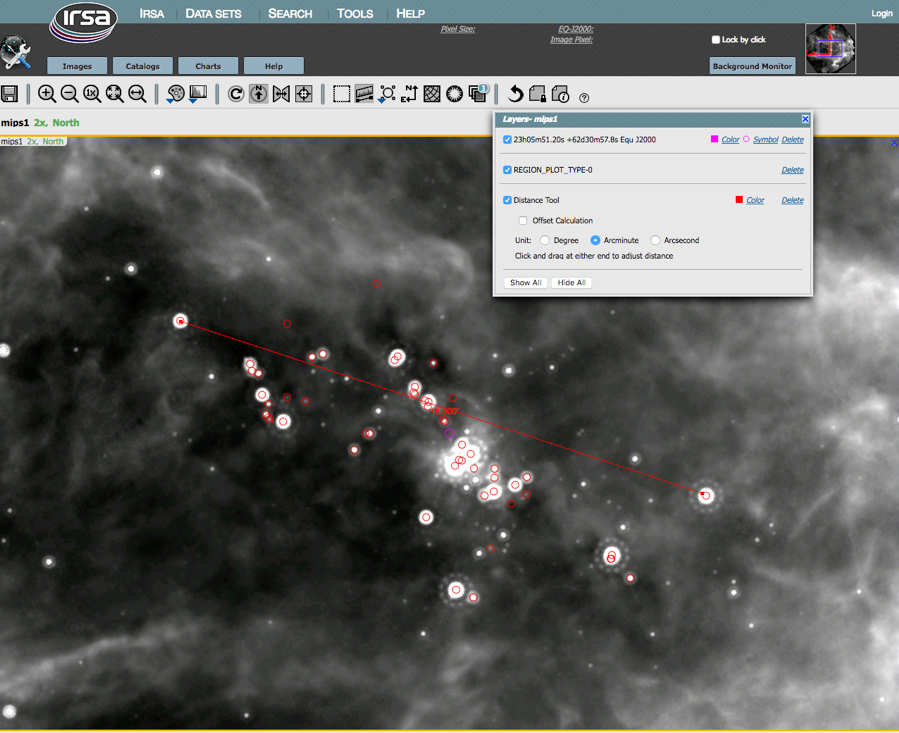
(2) Use IRSA tools to measure the length. Load an image into IRSA Viewer. Overlay the regions file of the objects of interest. Use the ruler tool to measure the length of the area. I get 16 arcmin.

Distance2.png

(3) look at the min and max ra and dec in the file of our 54 interesting sources. Use spherical trigonometry to compute the difference. I have routines in IDL that do this for me, but you can also straightforwardly program a spreadsheet to do it.

  • The minimum ra for our sources is 346.19485 degrees
  • The maximum ra for our sources is 346.74532 degrees
  • The minimum dec for our sources is 62.436698 degrees
  • The maximum dec for our sources is 62.588064 degrees
  IDL> print, sphdist(min(data.ra), min(data.dec), max(data.ra), max(data.dec), /deg)

This calculation yields 0.29574128 degrees 

  IDL> print, sphdist(min(data.ra), min(data.dec), max(data.ra), max(data.dec), /deg)*60

This calculation yields 17.744477 arcminutes

So, no matter how we do it exactly, it’s always about 16-18 arcmin.

Finding the "true" size.

Now, we have a long, thin triangle: Distance3.png

The physical size, D, is given by the following formula: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D= \frac{\theta}{206265} d} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \theta} is the size of the object in arcseconds, d is the distance to the object, and there are 206265 arcsec/radian.

  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \theta} we have just measured to be 16 arcminutes = 16 arcmin * 60 arcseconds/arcmin = 960 arcseconds
  • d = 700 pc
  • D = (960 / 206265) * 700 = 3.26 pc
  • 1 pc is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3.086 \times 10^{13}} km
  • 3.26 pc= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8.11 \times 10^{12}} km
  • Going back to our spreadsheet from the spring, we found that the Kuiper Belt is about 6Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \times10^9} km.
  • So, I get ~1350 KBs across.

These are not super precisely known numbers, so “about 1300 KB diameters” is just fine of an answer.

Retrieved from "https://vmcoolwiki.ipac.caltech.edu/index.php?title=Finding_the_diameter_of_a_region_we_care_about&oldid=13455"